Logarithmic derivative of wave function

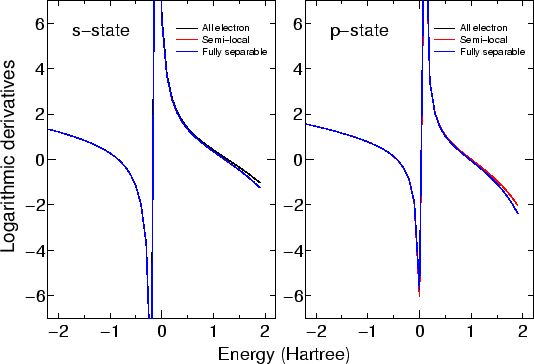
To check the transferability of generated pseudopotentials, a useful measure is to compare logarithmic derivatives of wave functions [16]. If the logarithmic derivative of pseudopotential is comparable to that by the all electron calculation through a wide range of energy, then the pseudopotential would possess a good transferability. In Fig. 4 shows the logarithmic derivatives in a carbon atom, indicating a good transferability of the pseudopotential. The keywords concerned to the calculations of the logarithmic derivative are as follows:

• log.deri.RadF.calc

  When the logarithmic derivatives are calculated, then ON, otherwise, OFF.

• log.deri.MinE

  The lower bound of energy (Hartree) used in the calculation of logarithmic derivatives of radial wave functions.

• log.deri.MaxE

  The upper bound of energy (Hartree) used in the calculation of logarithmic derivatives of radial wave functions.

• log.deri.R

  Radius at which the logarithmic derivatives of radial wave functions are evaluated.

You can find details for these keyword in the section, Input file. In case of log.deri.RadF.calc=ON, calculated logarithmic derivatives are output in files *.ld#, where * is the file name that you specified by the keyword, System.Name, and # is the angular momentum number. If the fully relativistic calculation is performed as 'eq.type=dirac', the file name is *.ld%_#, where % runs 0 to 1 corresponding to $j=l+1/2$ and $j=l-1/2$, respectively.

Figure: Logarithmic derivatives of radial wave functions under the all electron potential, semi-local pseudopotential, and fully separable pseudopotential of a carbon atoms