Next: In case of non-collinear Up: Unfolding method for band Previous: The origin of the Contents Index
The unfolded spectral weight can be visualized by an intensity map
that the weight ![]() is smeared out by a Lorentian function:
is smeared out by a Lorentian function:
(1) Compilation of intensity_map.c
In the the directory 'source', please compile 'intensity_map.c' as
gcc intensity_map.c -lm -o intensity_mapand copy the executable file 'intensity_map' to your work directory.
(2) Generation of the intensity map
After finising the unfolding calculation, you can generate a file storing a mesh data
for drawing the intensity map using 'intensity_map'.
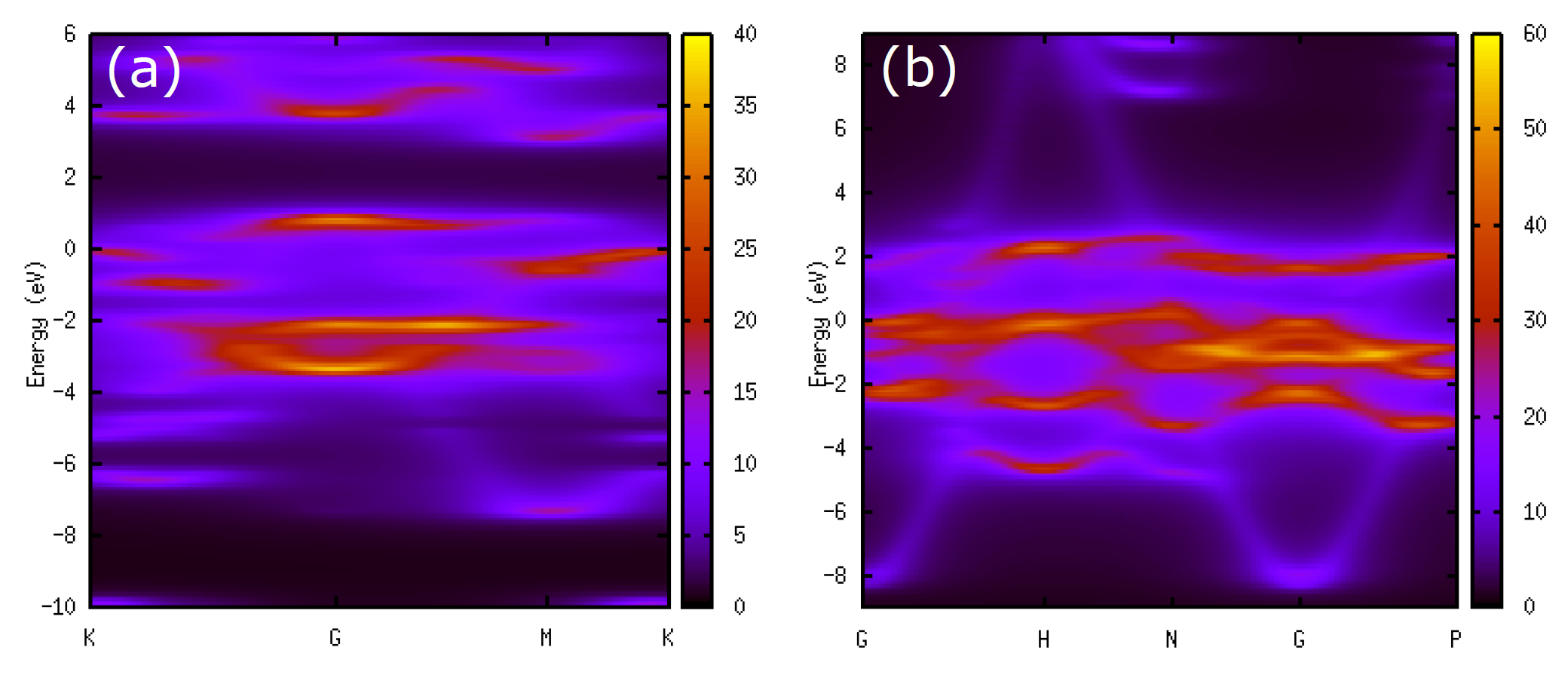
For the case of SiC (![]() ) supercell in a two-dimensional honeycomb structure
with a Si vacancy discussed in the previous subsection, where the input file is 'SiC_C_SP_V.dat',
e.g., one can generate a file 'sic-intmap.txt ' storing the mesh data by
) supercell in a two-dimensional honeycomb structure
with a Si vacancy discussed in the previous subsection, where the input file is 'SiC_C_SP_V.dat',
e.g., one can generate a file 'sic-intmap.txt ' storing the mesh data by
./intensity_map sic_c_sp_v.unfold_totup -c 3 -k 0.1 -e 0.1 -l -10 -u 6 > sic-intmap.txtwhere the arguments have the following meaning:
-c column of spectral weight you analyze
-k degree of smearing (Bohr^{-1}) in k-vector
-e degree of smearing (eV) in energy
-l lower bound of energy for drawing the map
-u upper bound of energy for drawing the map
You might be confused by the argument '-c' specifying the column number in the file.
When you analyze 'System.Name.unfold_orbup(dn)', you will refer the sequence number for
pseudo-atomic orbitals in 'System.Name.out'. Then, it should be noted that the number
(3) Drawing of the intensity map
Using gnuplot you can draw the intensity map.
For example, for the calculation with the input file 'SiC_C_SP_V.dat' it can be done
as follows:
gnuplot> set yrange [-10.000000:6.000000]
gnuplot> set ylabel 'Energy (eV)'
gnuplot> set xtics('K' 0.000000,'G' 0.722259,'M' 1.347753,'K' 1.708883)
gnuplot> set xrange [0:1.708883]
gnuplot> set arrow nohead from 0,0 to 1.708883,0
gnuplot> set arrow nohead from 0.722259,-10.000000 to 0.722259,6.000000
gnuplot> set arrow nohead from 1.347753,-10.000000 to 1.347753,6.000000
gnuplot> set pm3d map
gnuplot> sp 'sic-intmap.txt'
 |