Two sorts of the initial approximate Hessian for the RF and EF optimizers in the geometry optimization
are available in OpenMX Ver. 3.8, which can be specified by the following keyword:
MD.Opt.Init.Hessian Schlegel # Schlegel|iden, default=Schlegel
The defaut is 'Schlegel' which was proposed by Schlegel [50], and estimates the initial Hessian
using a simple model consisting of bond stretching, angle bending, and torsion, while only the bond stretching term
is taken into account in the implementation of OpenMX Ver. 3.8.
The other is 'iden' which starts from the identity matrix for the approximate Hessian.
In both the cases, the initial Hessian is updated every geometry optimization step by
the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method [49].
It is noted that 'Schlegel' is not supported for the optimizers of 'BFGS' and 'DIIS'.
In general, the method of Schlegel provides a faster convergence in the optimization compared to the initial
approximate Hessian of the identity matrix. Thus, one should use 'Schlegel' being default as a first choice.
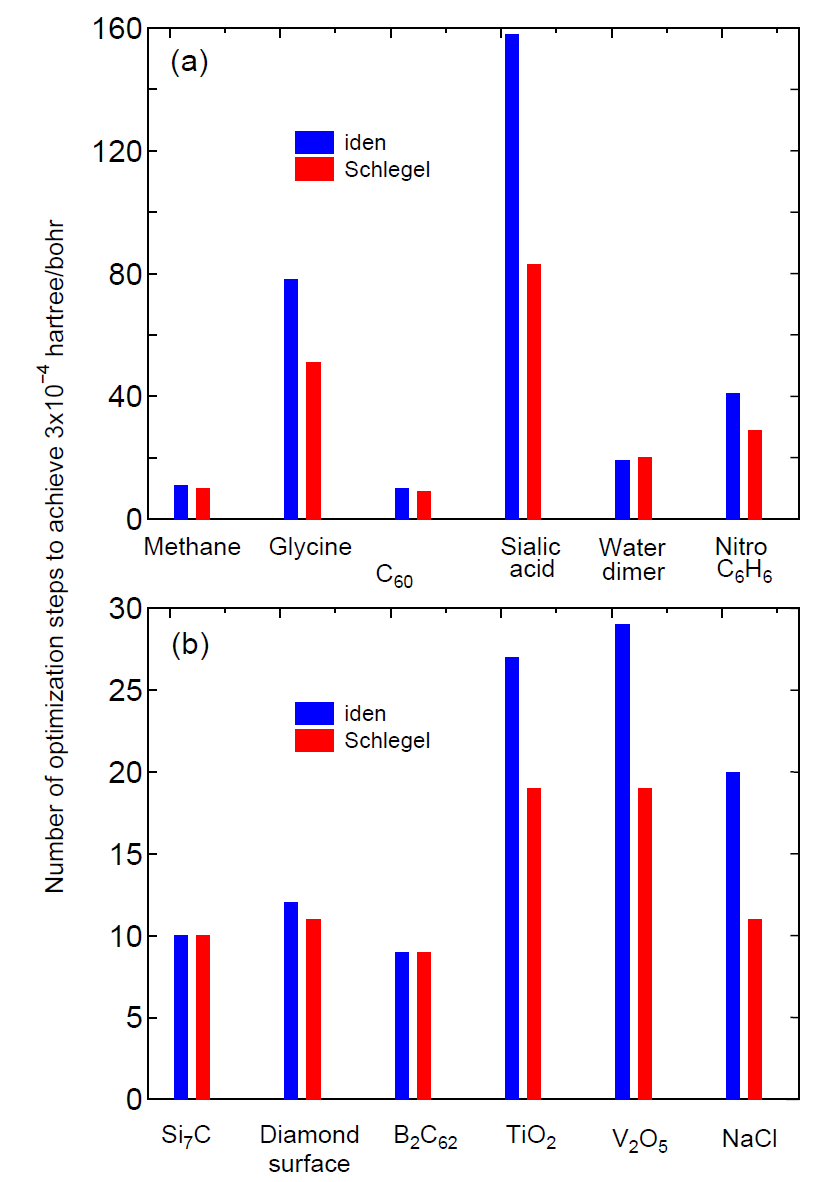
In Fig. 11 a comparison between 'Schlegel' and 'iden' is shown during the geometry
optimization using the EF method. It can be seen that the EF method with 'Schlegel' is faster than 'iden'
in most cases including molecules and bulks.
Figure 11:
The number of optimization steps to achieve the maximum force of below
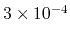 Hartree/Bohr
for (a) molecular systems and (b) bulk systems using the RF method with the initial Hessian of 'iden' and 'Schlegel'.
Hartree/Bohr
for (a) molecular systems and (b) bulk systems using the RF method with the initial Hessian of 'iden' and 'Schlegel'.
 |
2016-04-03
