Next: For calculations with lots Up: Density of states Previous: Density of states Contents Index
The density of states (DOS) is calculated by the following two steps:
(1) SCF calculation
Let us illustrate the calculation of DOS using the carbon diamond. In a file 'Cdia.dat' in the directory 'work', the keywords for the DOS calculation are set to
Dos.fileout on
Dos.Erange -25.0 20.0
Dos.Kgrid 12 12 12
In the specification of the keyword 'Dos.Erange',
the first and second values are the lower and upper bounds of
the energy range (eV) for the DOS calculation, respectively,
where the origin (0.0) of energy corresponds to the chemical potential.
Also, in the specification of the keyword 'Dos.Kgrid',
a set of numbers (n1,n2,n3) is the number of grids to
discretize the first Brillouin zone in the k-space,
which is used in the DOS calculation.
Then, we execute OpenMX by:
% ./openmx Cdia.dat
When the execution is completed normally, then you can find files
'cdia.Dos.val' and 'cdia.Dos.vec' in the directory 'work'.
The eigenvalues and eigenvectors are stored in the files
'cdia.Dos.val' and 'cdia.Dos.vec' in a text and binary forms, respectively.
The DOS calculation is supported even for the O(
(2) Calculation of the DOS
Let us compile a program package for calculating DOS. Move the directory 'source', and then compile as follows:
% make DosMain
When the compile is completed normally, then you can find
an executable file 'DosMain' in the directory 'source'.
Please copy the file 'DosMain' to the directory 'work',
and then move to the directory 'work'.
You can calculate DOS and projected DOS (PDOS) using
the program 'DosMain' from two files 'cdia.Dos.val'
and 'cdia.Dos.vec' as:
% ./DosMain cdia.Dos.val cdia.Dos.vec
Then, you are interactively asked from the program as follow:
% ./DosMain cdia.Dos.val cdia.Dos.vec
Max of Spe_Total_CNO = 8
1 1 101 102 103 101 102 103
<cdia.Dos.val>
<cdia>
Which method do you use?, Tetrahedron(1), Gaussian Broadeninig(2)
1
Do you want Dos(1) or PDos(2)?
2
Number of atoms=2
Which atoms for PDOS : (1,...,2), ex 1 2
1
pdos_n=1
1
<Spectra_Tetrahedron> start
Spe_Num_Relation 0 0 1
Spe_Num_Relation 0 1 1
Spe_Num_Relation 0 2 101
Spe_Num_Relation 0 3 102
Spe_Num_Relation 0 4 103
Spe_Num_Relation 0 5 101
Spe_Num_Relation 0 6 102
Spe_Num_Relation 0 7 103
make cdia.PDOS.Tetrahedron.atom1.s1
make cdia.PDOS.Tetrahedron.atom1.p1
make cdia.PDOS.Tetrahedron.atom1.p2
make cdia.PDOS.Tetrahedron.atom1.p3
make cdia.PDOS.Tetrahedron.atom1
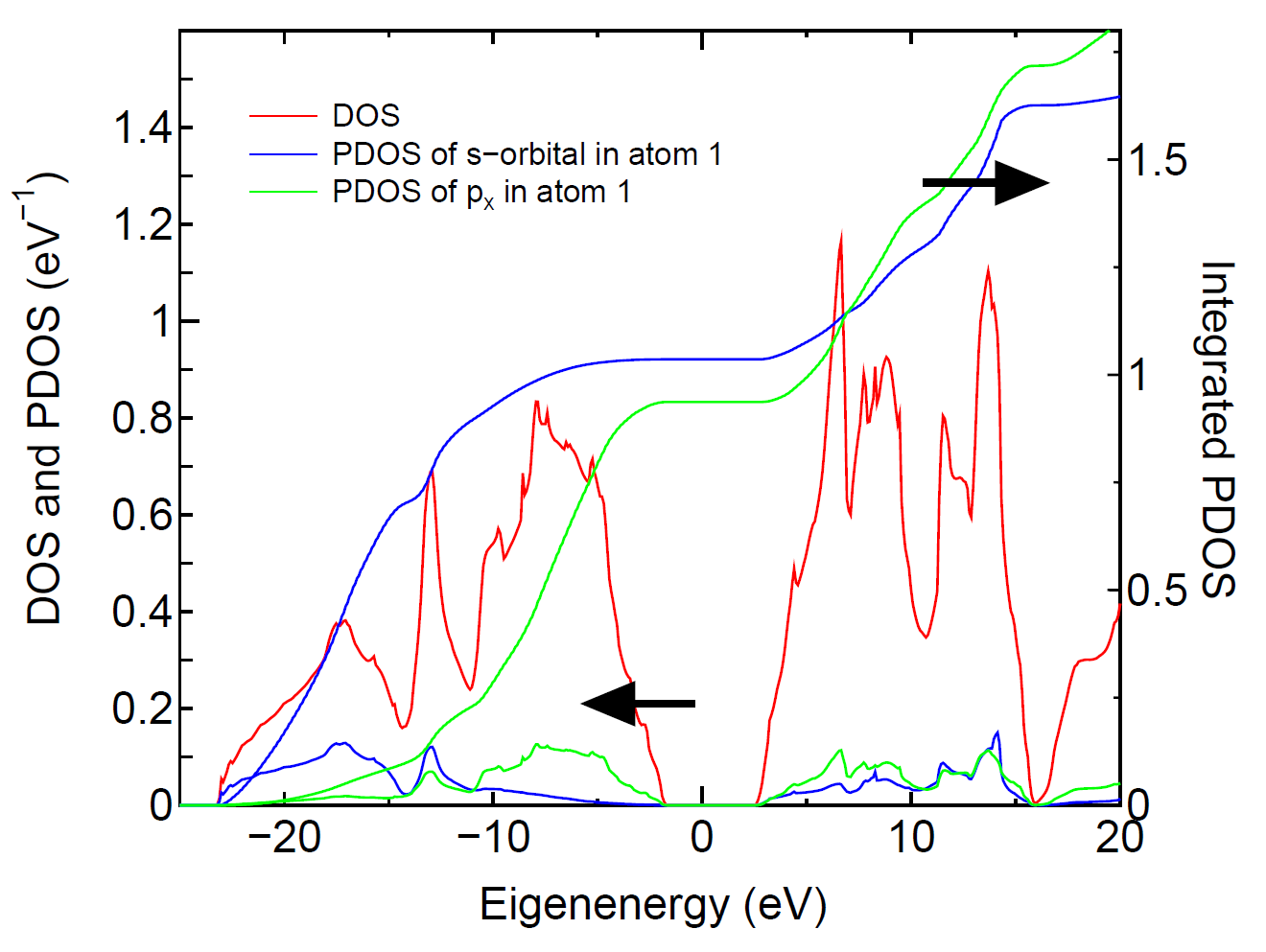
The tetrahedron [51] and Gaussian broadening methods
for evaluating DOS are available. Also, you can select DOS or PDOS.
When you select the calculation of PDOS, then please select atoms
for evaluating PDOS. In this case, each DOS projected on orbitals
(s, px (p1), py (p2), pz (p3),..) in selected atoms are output
in each file. In these files, the first and second columns are
energy in eV and DOS (eV
 |
2016-04-03